Gradient magnitude computation measures the intensity of change in pixel values. I first took the partial derivative in x (horizontal direction) and y (vertical direction) of an image by convolving the image with difference operators D_x and D_y. Then, the gradient magnitude was calculated by combining these two measures: square-rooting the sum of the x and y gradient components squared. [np.sqrt(grad_x**2 + grad_y**2)]

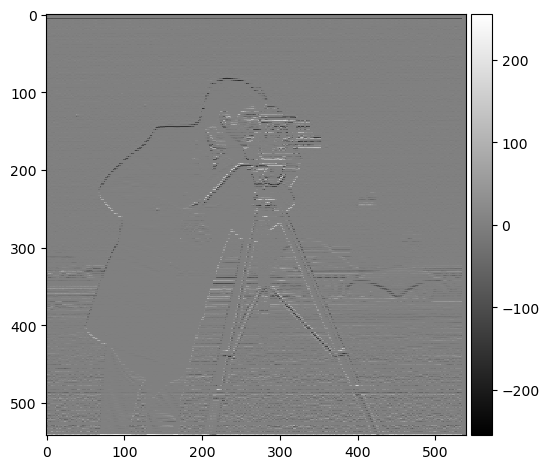

(dx, dy, gradient magnitude, binarized)
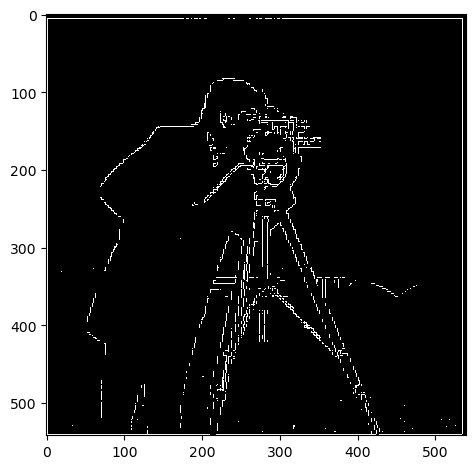
Below are the results from convolving the image with a gaussian and repeating the procedures in part 1.1: I saw that the binarized image had thicker lines than the one in part 1.1 since it's more robust to noise.



(dx, dy, gradient magnitude, binarized)
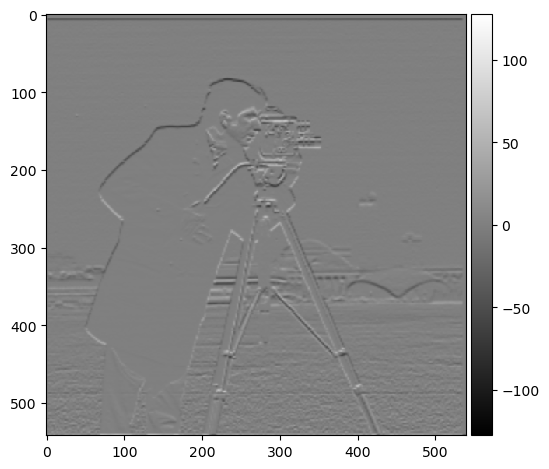
Below are the results from convolving the gaussian with D_x and D_y first: I got the same results as using the previous method. The edges were more defined.
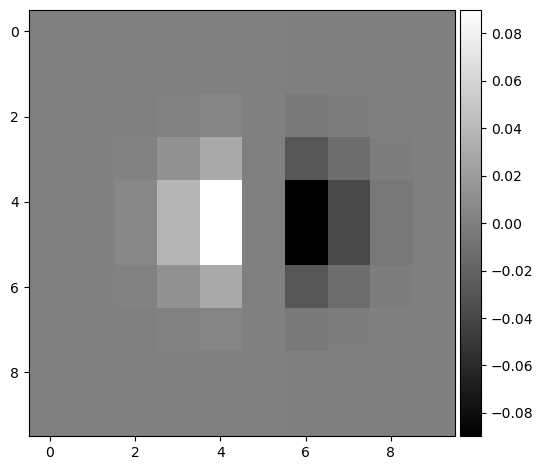
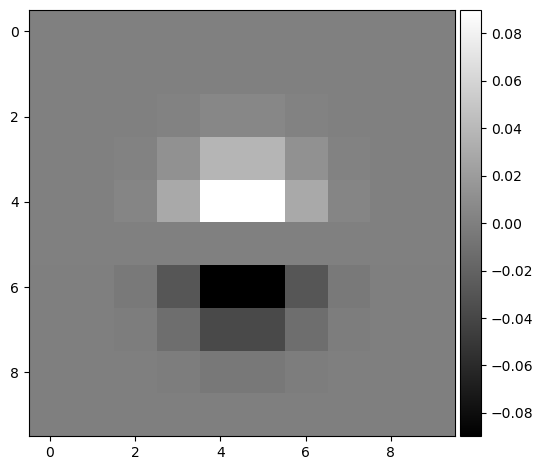




(dx_gaussian, dy_gaussian, dx, dy, gradient magnitude, binarized)
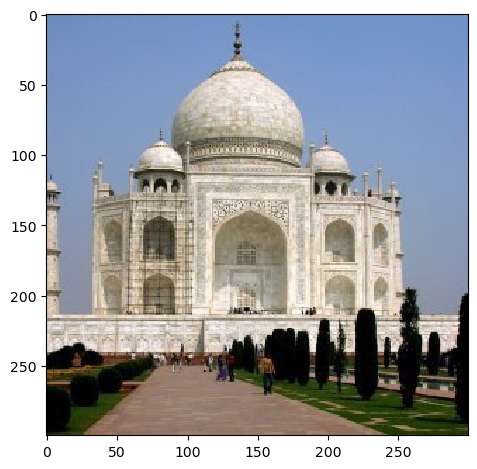
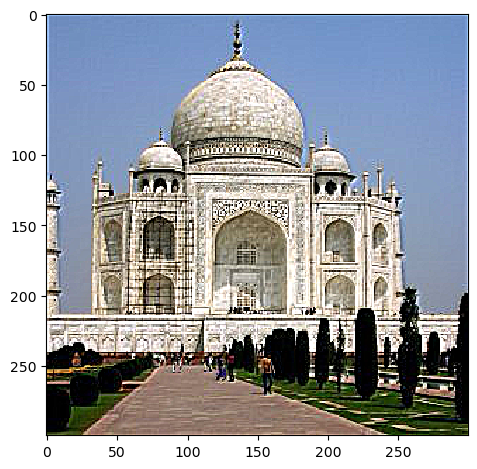
(before, after: alpha=3)


(before, after: alpha=3)
A sharp image of a bird, blurred it, and tried to sharpen it again:
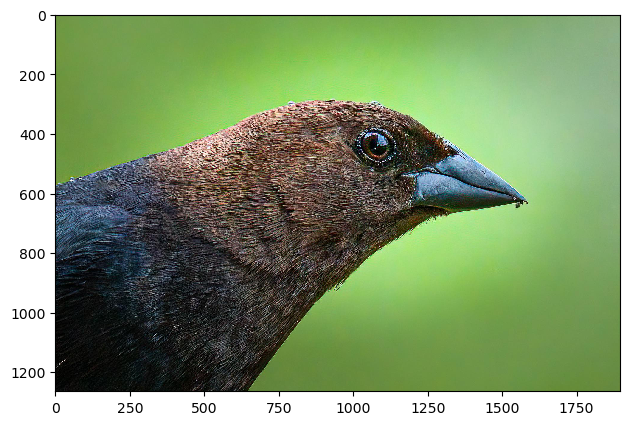

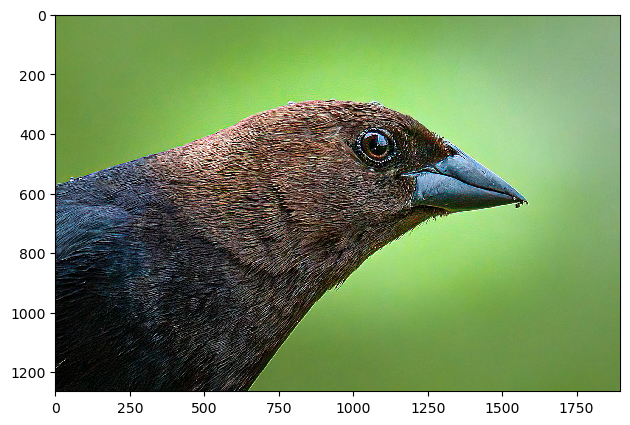
(original, blurred, sharpened: alpha=3)
Blending high frequency portion of one image with the low-frequency portion of another allowed us to create a hybrid image that had different interpretations at different distances.



(Derek and Nutmeg)
Below is an example of change over time:



(before, after, hybrid image)
Below is an example of morph between different objects (eagle and dog):
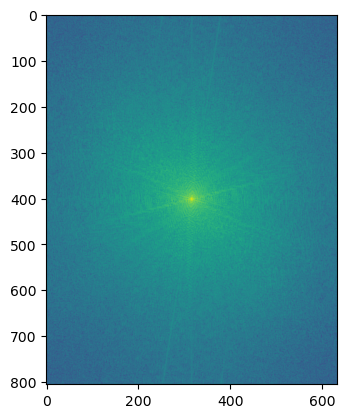
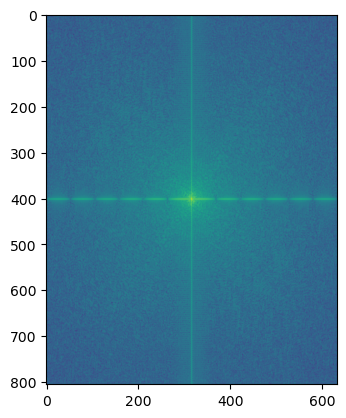
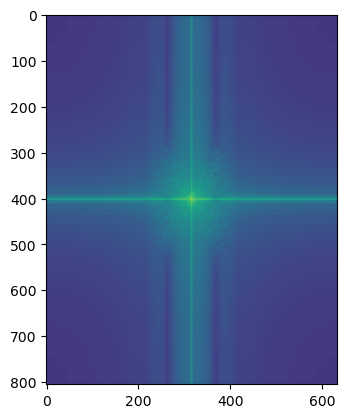
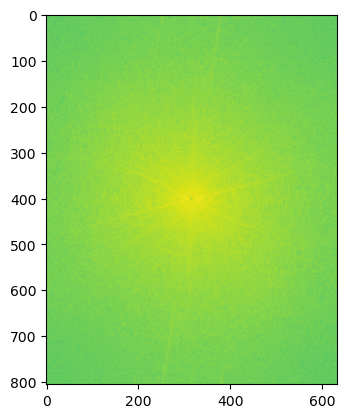
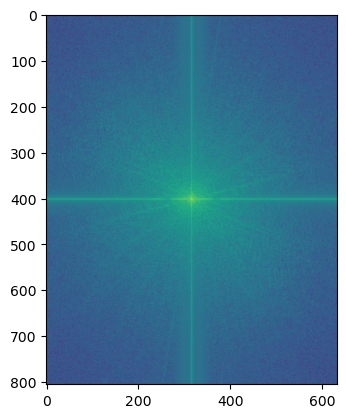
(Log magnitude of the Fourier transform of image 1, image 2, low-pass filtered image 1, high-pass filtered image 2, hybrid image)


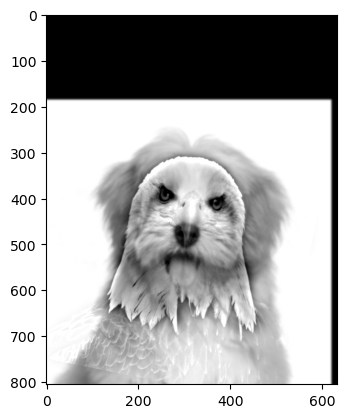
(eagle, dog, hybrid image)
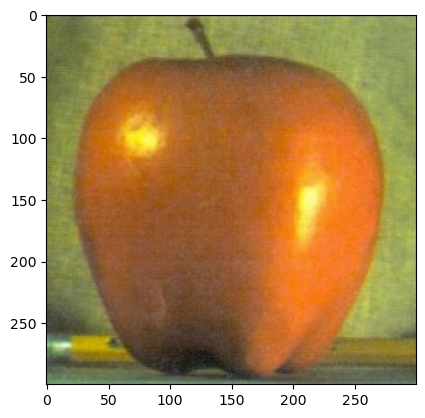
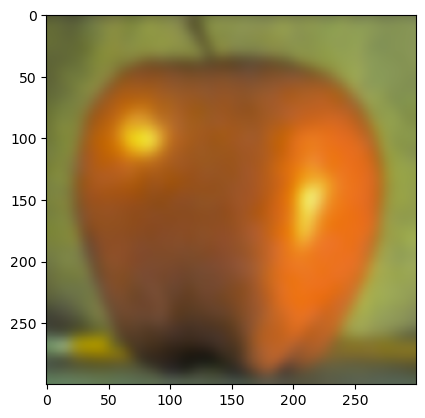
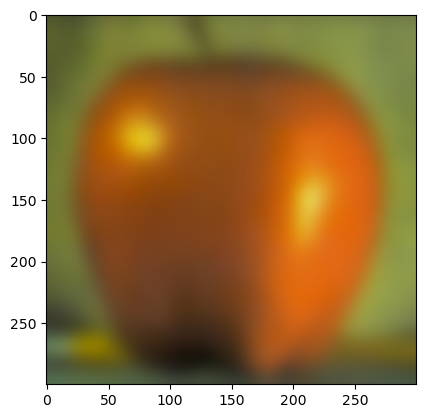
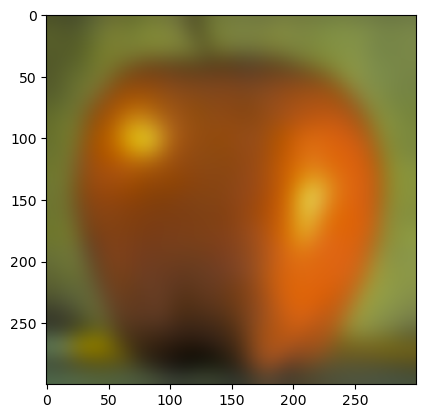
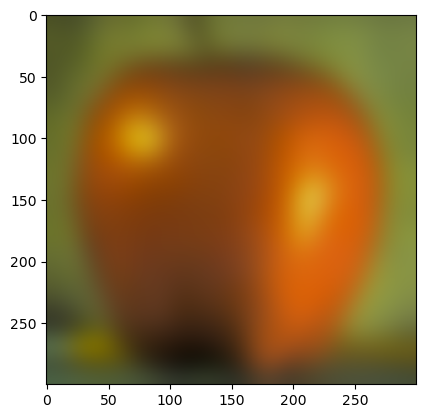
(Gaussian stack of apple)
(Laplacian stack of apple)

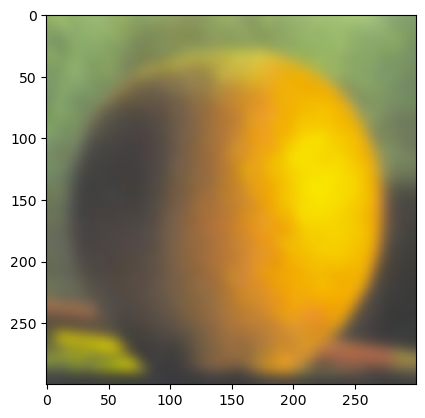
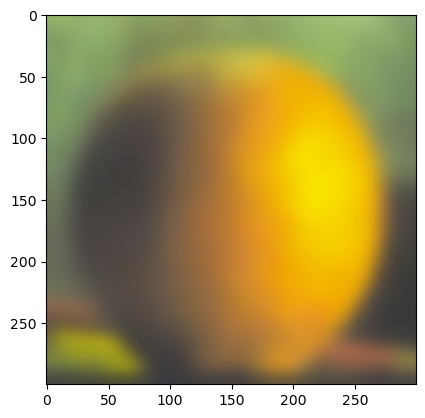
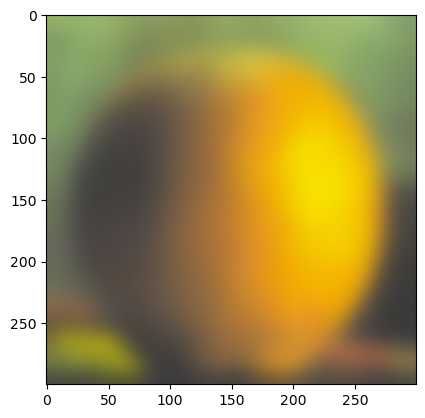
(Gaussian stack of orange)

(Laplacian stack of orange)


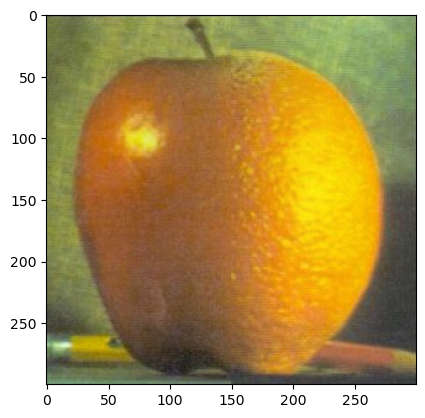
(Orange, Apple, Oraple)
Horizontal mask:


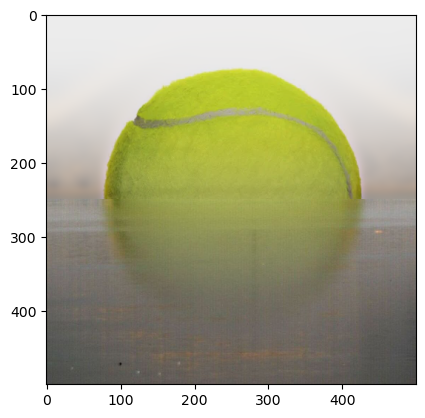
(tennis, arch bridge, blending)
Irregular mask: triangle



(sailing boat, desert, blending)